Mike's Chess Page - Info

This is some basic info about how the tool works. If you have any questions, feel free to ask.

How is the data stored?

Take a chessboard and slice it in eight.

The encoder enumerates every possibility, and gives each a number. It then selects one of the possibilities (0-1023), so that one slice of chessboard can respresent 10 bits of binary.

Of course, there are 8 slices, so this part of the algorithm can only store the first 80 bits.

Looking accross the chessboard, there is one more opportunity for re-arranging things:

There are 5040 ways to order these pieces, making them useful for another 12 bits (a number 0-4095). As there are both black and white rows, we can store the last 24 bits using the order of the more important pieces.

This is the order used to divide a string of binary:

Column a:      0000000000   (digits 1-10)
Column b:      1111111111   (digits 11-20)
Column c:      0000000000   (digits 21-30)
Column d:      1111111111   (digits 31-40)
Column e:      0000000000   (digits 41-50)
Column f:      1111111111   (digits 51-60)
Column g:      0000000000   (digits 61-70)
Column h:      1111111111   (digits 71-80)
Order (White): 000000000000 (digits 81-92)
Order (Black): 111111111111 (digits 93-104)

Calculating every combination takes a couple of seconds, so for speed it is cached in a text file. In this text file to be precise.

Because the order of combinations is important, just download the text file and parse it, it will save a lot of trouble! There is also the source code of this site (includes the code that generated that pesky file).

The decoder is the same process in reverse.

Is there a way to store more data than this?

Absolutely. The idea behind this method could be stepped up to assign a number to every combination possible on the entire board, it just hasn't been written efficiently yet.

Is there a different, human-readable algorithm?

You are right, the lookup table is far too much to print, memorise, or otherwise use without a computer. For those of us who simply want to use a chessboard instead of leaving a pen by the phone, look at this familiar picture:

1. In the centre of the board, there are 32 blank squares.
2. There are 32 pieces outside the blank space.
3. Simply place the pieces in the space to form a 32-bit string of binary.

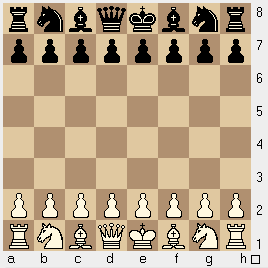
Unfortunately, even if you can encode hexadecimal or convert from decimal straight to binary in your head (it's not hard but most of us would really prefer a pen), you can only fit 8 or 9 (decimal) digits onto the board with this method. That's not even enough for most phone numbers!