Porting BASIC to my 6502 computer

I’ve recently been building my own 6502-based computer. After a lot of work on the hardware side, I decided that it’s time to move past “Hello World” programs, and port a BASIC interpreter.

Background

This computer is architecturally similar to a 1980’s home computer, where BASIC was a widely-used interpreted language. Porting an existing interpreter will be a fast way to get a command-prompt, and it will also add the ability to load arbitrary software, by typing out a program.

I heard about an interpreter called EhBASIC (“Enhanced BASIC”) from on this YouTube video by Chris Bird. It’s source-available (free for non-commercial use only), and seems to be well-regarded by 6502 enthusiasts.

EhBASIC was written by the late Lee Davidson. I based my port on the version v2.22, hosted on Klaus Dormann’s GitHub. I used Hans Otten’s mirror of Lee’s website as a reference, plus the EhBASIC section of the 6502.org forum.

Porting process

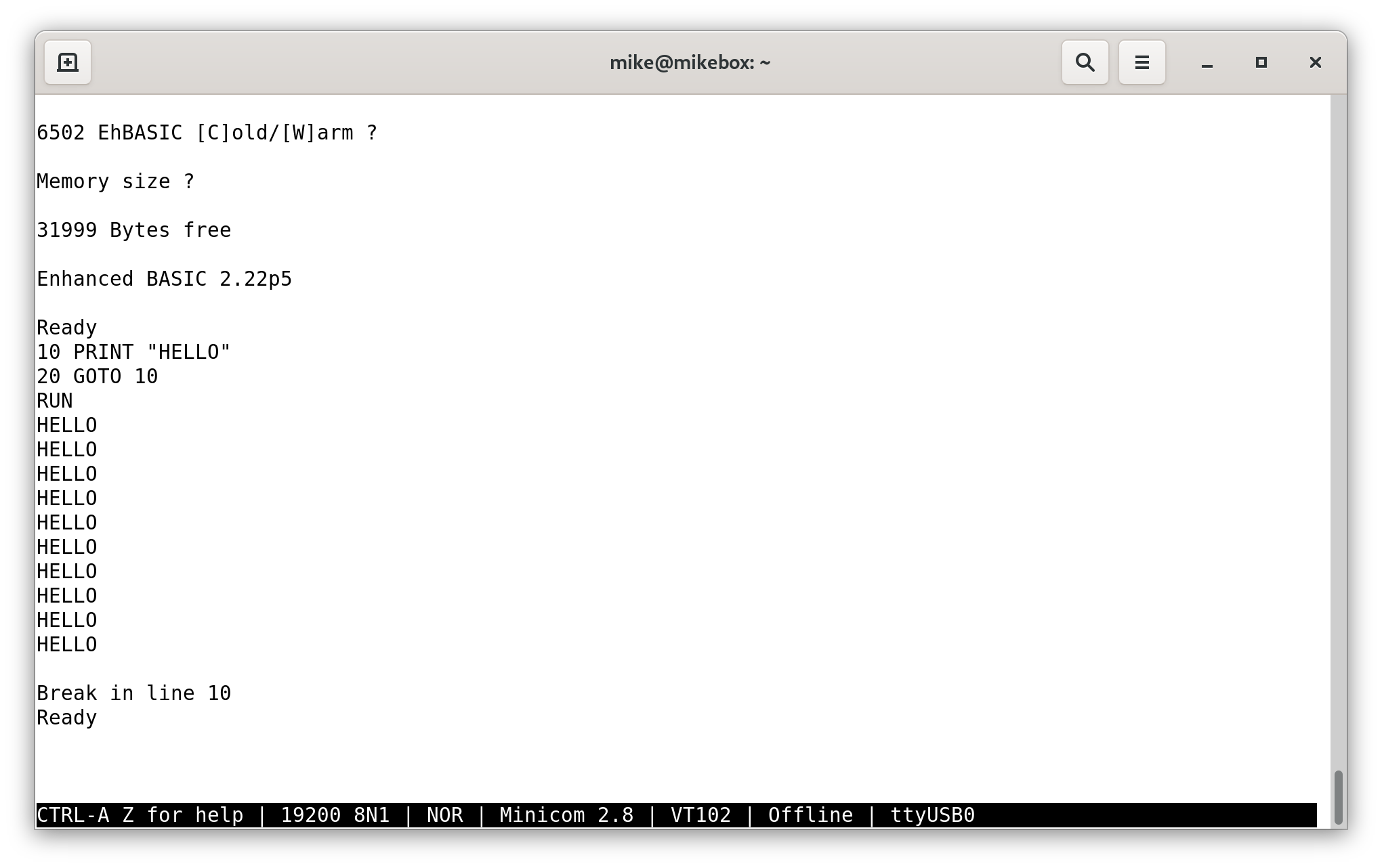
EhBASIC was a breeze to port.

I started with the ‘patched’ code from Klaus2m5/6502_EhBASIC_V2.22, which I placed in a local git repository, so that I could track the changes.

I first changed some of the syntax so that the code would assemble with ca65, since that is the assembler I’m using for everything else. There are other ca65 ports around, though they do not include the same patches.

The --feature labels_without_colons setting in ca65 was useful here, since the original source does not include colons after label names. The output was 10.5KiB of machine code, which will fit in the 16KiB of ROM space which I have available in my home-built computer.

I also confirmed that the code did not depend on using undocumented 6502 CPU opcodes, which would have been incompatible with my newer-generation 65C02 CPU.

Next, I dropped in the correct routines to read and write characters. I already had something similar from an earlier blog post. I needed to make some small changes to use the carry bit (SEC / CLC opcodes) to indicate whether a character had been received, and to set up the 6551 ACIA on startup. I programmed the code to an EEPROM, and it worked the first time.

All of my changes against the original code, including the Makefile and ca65 config file are in this commit. The memory addresses line up with the decoding scheme described here.

Wrap-up

BASIC is an interesting language, if only for historical reasons. Classic BASIC feels very clunky by modern standards, but the user experience is not that different to the modern Python REPL. Or at least, it is more similar than you might expect given how far computers have advanced.

I’m running EhBASIC on an 8-bit CPU, where the main alternative is plain 6502 assembly language. BASIC has allowed me to hit the ground running, and gives me access to floating point maths and user-loadable programs, on a computer that does not have an operating system or removable storage.

My home-built computer has a switch for selecting between two ROM’s. My plan is to write my own code in assembly language, but keep this port of EhBASIC in the secondary ROM, so that the computer can always boot to something that works.